1. «Ускорение» свободного падения, как явление полевой инверсии.

Напомним, что поле силы тяжести космических тел можно разделить на поворотные (инверсионные) поля силы тяжести (силы падения), как явно проявленные поля планет и отдельных спутников (например, Титана), и - на спиральные слабые поля спутников планет, астероидов и комет. Поворотные поля силы тяжести образуются наружно-молекулярной полевой оболочкой планет и их оболочковым (эллипсным) вращением вокруг окружного центра (считаемого неким «барицентром»), образующим их суточное вращение. Отчего эти поля и получают инверсионную или поворотную структуру вместе с образованием их вращения вокруг оси. У больших планет –это вращение их взаимно-центрической орбиты с полевой сферой ретроградных спутников вокруг их окружного центра, спрятанного внутри их газовой оболочки. Спиральные же слабые поля образуются у космических тел за счёт их наружно-молекулярной полевой оболочки, вращающейся вместе с телом вокруг окружного центра, из-за чего эти тела не получают и одно-центрового вращения вокруг оси, как оси тела (подобно юле). Вот потому, например, спутники, космические аппараты и астероиды вращаются, двигаясь только по окружности, т.е. не имеют собственного вращения вокруг оси, как такового. 

В связи с выше изложенным и у Луны, также вращающейся вокруг её окружного центра, интенсивность её поля силы тяжести составляет величину (в виде «ускорения» свободного падения) намного меньшую принятой в теории гелиоцентризма. И, исходя из месячного лунно-земного вращения и меньшего примерно в 3,6 раза диаметра Луны её весовая гравитация составляет лишь около 9 % от интенсивности поля силы тяжести Земли ((9,8/30)/3,6), чем примерно в 11,5 раза меньше земной весовой гравитации. Т.е. тело, имеющее вес на Земле в 100 кг., на Луне будет весить всего около 9 кг., падая по явно спиральной или параболической траектории (сразу в сторону). И можно сказать, что поворотное или явное поле силы тяжести, как поле одно-центровое, проявляет именно окружной объём пространства.  Подобно и магнитное поле уже в массовой полевой фазе пространства, как также одно-центровое, явно проявляется лишь у планет, имеющих вращение вокруг их внешнего окружного центра (образующего их годовой оборот).
Отсюда и заряд поля силы тяжести («ускорение» свободного падения) «g», переходящий в заряд поля планетного вращения, можно рассматривать относительно трёх видов полевых объёмов. В старой физике совершенно необоснованно и искусственным образом уравнивают силу тяжести (что есть в реальности уже работой силы тяжести) «F=m*g» с формулой «G*(m*Mз)/R^2», исходящей из неверного понимания гравитации взаимодействием двух масс, где m и Mз – масса соответственно тела и Земли, но не различаемые фактически от категории веса (см. 5, стр.126). В реальности же величина «g» находится не из такого надуманного равенства, а - из формулы высоты падения «h» Галилея «g=2h/T^2» и из формулы оборотного маятника «g=4пи^2h/T^2» (см. 4, стр. 906), где «h» -  расстояние между параллельными осями подвеса маятника. Кроме того, исходя из понимания величины «g» в старой физике центростремительным «ускорением» при определении космической скорости (см. 16, стр.73), величина «g» выражается, как «4пи^2R/T^2» (см. 16, стр.31), где «R» –радиус вращения. Отсюда при равенстве во всех формулах периода «T» одной и той же величине, как приведённой единице, возникает тождественное выражение «2h≡4πи²h≡4πи²R»  или структурное преобразование «2h:4πи²h:4πи²R», которое однозначно указывает на инверсионную полевую структуру пространства. Т.е., расстояние между подвесами маятника «h» тождественно радиусу вращения «r», а высота падения «h» тождественна выражению «2πи²R», где «пи» в квадрате означает сопряжение радианных поворотов «?и», как двух взаимно-центрических полевых поворотов в двух перпендикулярных плоскостях. 
 

Так вот относительно окружного объёма нашей массовой фазы пространства величина «g» выражается, как «4πи²R/T²»  или в виде «V^2/R», поскольку в старой физике центростремительное «ускорение» равно отношению квадрата скорости, как скорости вращения (2пиR/Т), к радиусу (см. 16, стр.30), что изображено на рисунке выше. Относительно переходного полевого объёма величина «g» принимает контурный вид g0 без числа «пи» «4пиR/T^2». Но всемирная гравитационная полевая структура пространства (в рассмотрении гравитона, как исходного узелка полевого пространства) говорит об обратной зависимости от квадрата радиуса. Потому относительно сферического полевого объёма величина «g» выражается в виде «4πи²/T²» , т.е. – в размерности частотной силы падения и силы вращения (1/сек^2). Этим для размерной величины, равной единице (например, одному метру), заряд поля силы тяжести (силы падения) относительно плоского (вне-объёмного) восприятия в нашей фазе пространства становится частотой 3,13 «1/сек», как корень квадратный из величины «g». Т.е. «ускорение» свободного падения – это в полевой реальности пространственно-полевая частота.
 
А это значит, что величина «g» воспринимается «ускорением» свободного падения, а падение – неким равноускоренным движением только при определении скорости и высоты падения, когда падающее тело вступает в контакт с поверхностью, или, например, фиксируется его положение лазером. Этим проявлением общего дуализма инверсионно-полевой структуры пространства обозначается и наша массовая фаза пространства. Иначе говоря, из-за пространственно-полевого перпендикулярного поворота «пи/2» (образующейся и в структуре падения, о чём речь дальше) общая для всех тел частота  «1/ T=vg» , одинаково увлекающая их в падение, при обозначении нашей полевой фазы пространства инвертирует уже в скорость вращения 2пиR*(1/Т), зависящую от полевого радиуса, а значит, - и от высоты падения. При этом и скорость вращения становится для нас уже линейной скоростью (по линии падения). 

Приведённое явление полевой инверсии сравнимо с принципом неопределённости в квантовой физике, когда при определении одного параметра (например, координаты частицы) другой параметр (например, импульс), как определимый уже только в плоскости, перпендикулярной к первой, воспринимается относительно неё неопределимым. Это явление поворотно-вращательной относительности в физике различения характеризуется вращательным параллаксом, как различной окружной скоростью на фоне единой частоты вращения, наблюдающейся в полевой плоскости, уже перпендикулярной к первой. Проявление поворотности (инверсионного свойства) полевого пространства обозначается и в опытах якобы изменению веса гироскопа после его вращения, в которых вовсе не уменьшается вес, а создаётся тяга на конце стержня, где закреплён гироскопа из-за стремления образуемой при этом сферы вращения к повороту.

Таким образом, то, что равномерное вращение каждой точки плоскости окружности согласно старой физике происходит якобы «с ускорением, направленным в каждой точке окружности её центру» (см. 16, стр. 29) – это следствие иллюзии вращательного параллакса, как свойства дискретности нашей полевой массовой фазы пространства. Здесь, как и в принципе неопределённости, когда второй параметр становится неопределимым при установлении первого, движение, определённое равномерным в виде общей частоты вращения, после определения радиуса вращения, т.е. при выделении конкретной точки в общем вращении, вдруг получает разную скорость. При этом изменение периода вращения точки на окружной плоскости относительно другой точки приводит к иллюзии её отставания или опережения, как к иллюзии её отдельного вращения, что и происходит при наблюдении планет относительно солнечно-земного вращения. Изменение же самого радиуса точки относительно единого периода вращения окружной плоскости (как единой частоты) приводит в таком полевом повороте «?и/2» к иллюзии изменения её скорости, но что необоснованно называется неким «равноускоренным» движением. Квантовый, а точнее полевой эффект наблюдается потому и в наблюдении процесса падения, когда при определении отметки высоты уже не определима (напрямую не регистрируется) скорость падения.

Скорость при падении действительно зависит от высоты падения, причём – инверсионно или по параболическому закону (что показано ниже), причём – только при определении этой высоты (например, в результате контакта с опорой). Но это никак не изменение категории ускорения в старой физике, поскольку выражение величины «ускорения» (в реальности заряда вращения) и в виде «V^2/R» и в виде «4пи^2R/T^2» исключает возможность её изменения при изменении радиуса. Ведь одна и та же величина не может одновременно и расти, и уменьшаться, называясь то центростремительным, то центробежным «ускорением». Об этом свидетельствует и величина «g», которая вовсе не изменяется пропорционально высоте падения, а зависит лишь от расстояния до центра Земли, причём - от квадрата этого расстояния (как выражения полевой взаимо-центричности). В этой связи абсурдны и сами понятия центростремительного и центробежного ускорения, а так называемые центробежные и центростремительные силы – это в реальности обозначения контурных и частотных полевых окружностей, образующих сферу вращения и переходящих или инвертирующих друг в друга (см.5, стр. 215).

И напомним, что абсурдно в старой физике и вообще само понятие ускорения, как скорости изменения скорости, поскольку по размерности физики различения (инверсионно-полевой механики) эта величина обозначает уже работу силы и заряд силовой полевой сферы, аналогичный заряду поля силы тяжести (силы падения). Абсурдно потому и определять силу произведением массы на такое ускорение. Т.е. применяемая в старой физике категория ускорения (как скорость изменения скорости) отсутствует в природе. Ускорение, как и замедление – это изменение скорости за определённое время, которое неизменно для характеристик данного процесса, приводящее к инерционным (также полевым) явлениям, например, в виде перегрузок, но никак не скорость изменения скорости. В связи с вышеизложенным пространственно-полевой переход (п-п переход) исходной магнитной структурной частоты 10^6 наиболее явно проявляется в структуре траектории падения тела, поскольку это явление все могут наблюдать в любое время.

2. Полевой дуализм «и-п» структуры пространства на примере падения и о скорости падения.

Гравитационное течение, увлекающее все тела, образовано не некими мельчайшими частицами, поскольку в этом случае они проходили бы через массу, как через решето, а объёмное и структурное полевое течение, перпендикулярно развёрнутое к полевой структуре массы, чем и увлекает её. Падение в нашей окружной полевой фазе пространства с её окружным объёмом мы привыкли воспринимать также одно-центровым движением тел к центру Земли в каждой точке земной поверхности. Но, оказывается, это лишь иллюзия нашего восприятия, стоит лишь рассмотреть хотя бы причину появления числа «два» в знаменателе формулы пути падения. 
Путь падения «h», исходя из того, что величина «g» выражает в старой физике понятие «ускорения», как отношение изменения скорости к длительности этого изменения, должна выражаться в виде «h=g*t^2». Но в знаменателе появляется «двойка» именно потому что, величина «g», выражая полевое движение вращения, относится к вращению, т.е. – к полевой окружности «2пиR», образуемой её контурной (силовой) и частотной полуокружностями, перпендикулярными друг к другу. Этим определяемая высота падения по отношению к величине «g» или в повороте «пи/2» (на 90 градусов) – это обозначение второй части полевой окружности, как контурной полуокружности «пиR=h». Т.е., траектория падения, воспринимаемая нами прямой линией, - это в реальности длина дуги земной окружности (близкой к прямой линии), причём по отношению к заряду поля силы тяжести «g» формулой «h=g*t^2/2» мы определяем в реальности из-за полевого поворота «пи/2» длину полуокружности с диаметром, равным расстоянию между точкой начала падения и точкой контакта тела с поверхностью. Отсюда путь падения в нашей массовой фазе пространства – это не замеряемая высота, и не диаметр поворотной полевой окружности, а радиус такой полуокружности. Вот именно потому любое падающее тело и стремится вращаться. Т.е., на полевом, реальном уровне (предмассового полевого пространства) появление «двойки» в знаменателе формулы «h=g*t^2/2» объясняется возникновением полевой полуокружности вместо полной окружности.

Т.о., если выразить величину заряда поля силы тяжести «g» произведением контурной величины этого заряда g0 на число «gи», то путь падения преобразуется уже в радиус, как в половину указанного расстояния (πR=g*t²/2: R=g₀*t²/2), чем определяемая высота падения не только сокращается вдвое, но – и на величину «пи». Надо обратить внимание и на то, что поскольку диаметр в полу-вращении проявляется радиусом, то путь падения образуется полевым взаимно-центрическим вращением полевых сфер вокруг друг друга, общий диаметр качения которых растёт вместе с увеличением пути (см. рисунок ниже слева). И в моментальной фотографии нашей фазы пространства эта структура вращения представляет собой полевой дипольный или восьмеричный вид с общим диаметром, как с ожидаемым путём падения (исходя из формулы «h=g*t^2»). Но при контакте тела с опорой (при прекращении падения) такая структура складывается в одну полевую окружность, составленную уже из двух сложенных полуокружностей, диаметр которых равен радиусу предыдущего дипольного образования, как половины ожидаемого пути падения (см. рис. ниже справа). Образование полевой окружности падения доказывается и самим фактом колебания маятника. 
 

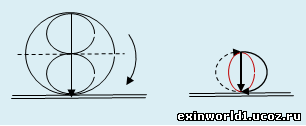При этом и радиус полевой полуокружности (как реально определяемый путь падения) с ростом высоты падения проявляется в виде уже длины окружности, перпендикулярно (на радианную величину «пи/2) развёрнутой к этому радиусу и, соответственно, - к наблюдателю, что показано красной окружностью на рис. выше. Ведь при контакте тела с опорой после падения (например, в виде удара) образуется силовая полевая сфера, состоящая из двух перпендикулярных друг к другу уже сферических образующих, как полных окружностей. Этим радиус падения образуется перпендикулярно к нему развёрнутой полевой окружностью, как сферической контурной образующей. Т.е. падение тела образуется полевой полуокружностью (проявляемой радиусом падения) и полной полевой окружностью (что и образует радиус падения), но перпендикулярно направленными друг к другу. Именно полная полевая окружность и увлекает полевое взаимно-центрическое вращение в движение падения, чем проявляется полевая наружно-молекулярная оболочка Земли, как составляющая (вместе с оболочковым или эллипсоидным лунно-земным вращением) в образовании поля силы тяжести. При этом значение радиуса падения, численно равное контурной величине «g0», что есть выражением полевой окружности (как сферической образующей) единицей взаимодействия, даёт величину около 19,6 м. (см. 5, стр. 114). 
Отсюда можно сказать, что лишь до высоты падения 19,6 м., примерно соответствующей и высоте опытов Галилея, проявляется действие формулы «h=g*t^2/2», которой определяется время падения, и - для определения скорости падения. До этой полевой высоты (которая воспринимается нами высотой вертикальной) скорость падения должна определяться через  инверсию пути падения именно в линейное расстояние в виде отношения к числу «пи», т.е. V = (h/пи)/t. Вот потому, если величину «g» в формуле «пR= g*t^2/2» выразить формулой оборотного маятника (g=4п^2R/T^2), то появляется инверсионное тождество «R≡2πR» . Здесь радиус, как расстояние между точками подвесов двух маятников (образующих оборотный маятник), означает как раз путь падения в виде расстояния между точкой начала и окончания падения, но становящегося относительно величины «g» уже длиной этой полевой окружности. В связи с этим путь падения на высотах, превышающих величину около 19,6 м., в структурной или в инверсионной записи выглядит, как «πR: (D) R: 2πR». А этим проявляется полевой дуализм падения, поскольку путь траектории падения, воспринимаемый нами прямой линией, в отношении к величине «g» становится полуокружностью, а затем (при определении скорости падения) и радиусом, который можно назвать инверсионным радиусом падения. Отсюда, чем больше путь падения, тем более отчётливо проявляется приведённая его структурная инверсия в виде полевой полуокружности, образуемой полной полевой окружностью, перпендикулярно развёрнутой к первой, что как раз и создаёт иллюзию некоего «равноускоренного движения». 

Т.о., можно сказать, что путь падения тела, воспринимаемый нами близким к прямой линии, как к дуге земной окружности, в начальном рассмотрении и в полевой реальности представляет собой полуокружность, а замеряемое расстояние уже в воспринимаемой нами реальности окружного объёма означает диаметр «D», но инвертирующий в радиус «R» при контакте с опорой. Это значит, что полевые контурные и частотные образующие окружности вращения, как полевое дипольное или восьмеричное образование, в нашем окружном объёме пространства за счёт радианного поворота «пи» «свёртываются» вокруг горизонтальной оси в единую полевую окружность, диаметр которой инвертирует в радиус падения, как в путь падения. При этом инверсионное равенство радиуса пути падения дуге земной окружности соответствует понятию одного радиана, что означает срединное звено пространственно-полевого перехода в структуре падения, как объёмного полевого преобразования. А то, что инверсионный радиус падения становится длиной окружности, может быть только при условии образования радиуса падения этой окружностью, как уже перпендикулярно развёрнутой к наблюдателю и по отношению к инверсионному радиусу.  
Этим инверсионное тождество«R≡2πR» означает как раз радианный поворот «пи/2» в пространственно-полевом переходе. По этой причине путь падения с большой высоты по отношению к величине «g» при определении скорости падения уменьшается уже не и не в «2пи» раз, а в «4пи» раза (2*2пи) от ожидаемого расстояния в виде движения в нашем массовом пространстве (подобного движению качения ядра или мяча по поверхности). Иными словами, в «2пи» раза уменьшается линейная скорость падения по отношению к формуле «h=g*t^2/2», применяемой старой физикой для всех высот падения. При этом скорость падения, заметим, из-за поворотности полевого пространства проявляется только при контакте тела с опорой. И, хотя она определяется высотой падения, но не возрастает, а остаётся постоянной на всём пути падения, из-за чего и возникает невесомость при падении.

Итак, длина траектории падения с больших высот через контурную величину заряда поля силы тяжести «g0» записывается, как «h=g0*t:2/4». Выражение же «4пи» означает квадрупольный вид поля силы тяжести, подобный и структуре магнитного поля (как ощущаемого нами магнитного поля в виде уже окружного объёма) с тем отличием, что магнитное поле является в этом случае одно-центровым, а поле силы тяжести (поле весовой гравитации) имеет оболочковую инверсионную структуру, переходящую в поле планетного вращения. Отсюда, определив время падения по формуле Галилея «hо=g*t^2/2», где «hо» - это замеряемая высота, скорость падения (после высот в 19,6 метров) должна определяться по отношению к инверсионно-полевой величине высоты «h=hо/2пи». И, например, при прыжке парашютиста с высоты в 1000 метров, время его падения (если бы не открывался парашют) составит около 14,3 секунд. А скорость его падения будет равна примерно 11,1 м/сек. ((1000/ (2*3,14))/14,3), но не абсурду «предельной» скорости 53 м/сек в употребляемой старой физике даже с учётом сопротивления воздуха.

3.«И-п» переход падения в орбитальное вращение и структура оболочковой (эллипсоидной) полевой сферы. 

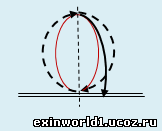
С увеличением высоты образование радиуса падения перпендикулярно к нему развёрнутой полевой окружностью, как сферической полевой окружностью (обозначенной на рис. ниже красным цветом), приводит ко всё большему искривлению пути падения в параболический вид, что показано на рисунке. Такой полевой инверсией объясняется и параболическая траектория, например, снаряда при выстреле. И на высоте около 160 км. путь падения, замеряемый нами дугой земной окружности, окончательно переходит в окружность с радиусом, примерно равным радиусу Земли (плюс высота в 160 км.). На полевом же уровне радиус падения становится полуокружностью, чем образуется уже полная окружность (на рис. ниже она обозначена штриховой линией). Этим прекращается падение, обозначая границу поля силы тяжести, и начинается орбитальное вращение, объясняясь тем, что высота границы поля силы тяжести образуется высотой около 40 км. над поверхностью Земли окружного радиуса Земли (считаемого «барицентром» в гелиоцентризме), как сферическим учетверением этого расстояния (о чём см. дальше).  
Можно сказать, что постоянное (с увеличением высоты) искривление радиуса падения образующей его (и перпендикулярной к нему) полевой окружностью на высоте около 160 км. приводит к его инверсии в полуокружность, чем возникает уже полная полевая окружность с обратным вращением (см. рис. ниже). А этим полевая окружность, образующая радиус падения (показана в красном цвете), инвертируется уже во фронтальное положение к наблюдателю, а полевая полуокружность становится перпендикулярной к наблюдателю контурной орбитальной окружностью. Т.е. инверсионный радиус падения на высоте около 160 км. полностью растягивается в полуокружность, чем становится явно проявленной (в её фронтальном виде) и полевая окружность в виде инверсионного тождества «R≡πR≡2πR». В связи с этим происходит новая полевая инверсия, проявляющая поле планетного вращения, как образование полного контурного вращения вокруг земной поверхности и уже - в плоскости, перпендикулярной к наблюдателю. И образуется такое орбитальное вращение полевой окружностью с диаметром, равным высоте до поверхности Земли, которую в этой связи можно назвать «высотной» окружностью. А поскольку орбитальная контурная окружность всё также должна образовываться синхронно (за то же время), что и «высотная» частотная («чисто» полевая) окружность, то этим и объясняется, что на низких орбитальных высотах оборот совершается всего за час с небольшим. При этом высотная окружность как бы стягивает орбитальную окружность с каждым оборотом, снижая её. Всё это наглядно показывает, что все проявления поля весовой гравитации – это инверсии полевой структуры, а не некое притяжение.
 

На высоте же геостационарной орбиты (около 36 тыс. км.) уже и «высотная» окружность также становится орбитальной окружностью, перпендикулярно направленной к самой орбите. Этим прекращается снижение или стягивание орбиты «высотной» полевой окружностью, которая вместе с орбитальной окружностью становятся частотной и контурной образующей полевой сферы планетного вращения. В связи с этим пространственные объёмы, образуемые выше 36 тыс. км. над земной поверхностью, можно назвать сферическими объёмами, от высоты 36 тыс. км. до границы поля силы тяжести – переходными пространственными объёмами, а от поверхности Земли до границы поля силы тяжести (точнее, поля силы падения) образуются окружные полевые объёмы.
То, что на полевом уровне радиус падения на границе поля силы тяжести (силы падения) становится полуокружностью и преобразуется этим в полную полевую окружность с обратным направлением, и вообще факт образования радиуса падения полевой окружностью означает возможность другой инверсии. Это преобразование радиуса падения в радиус выталкивания, как результат полевого поворота «?и» полевой полуокружности падения вокруг вертикальной оси. Иными словами, приведённая полевая структура образования пути падения объясняет факты инверсии поля весовой гравитации, как например, аномалии течения в иных местах жидкостей вверх (см. 5, стр.104). Приведённой инверсией полевой полуокружности падения в полуокружность выталкивания объясняется и движение вулканической магмы вверх из-под мантии Земли. Т.е. под земной мантией идёт именно такая инверсия поля весовой гравитации в нижнее поле силы тяжести (см.5, стр. 122).

Поворотная инверсия полевой полуокружности падения обозначает и структуру левитации, как преодоления силы тяжести. Это значит, что образование вокруг тела полевой сферы, обратно развёрнутой на величину «пи/2» вокруг вертикальной оси относительно поля силы тяжести прекращает действие этого поля, а полный поворот на величину «пи» вызывает обратное движение вверх относительно земной поверхности. Такой разворот в виде преобразования молекулярных полевых объёмов прослеживается на примере поднятия газов. На основе инверсионной структуры движения падения указанный пространственно-полевой переход в последовательности его постоянных преобразований в начальном виде можно выразить образованием взаимно-центрического сопряжения двух сферических объёмов, что и образует исходное солнечно-земное вращение (и, например, лунно-земное вращение). И проявляется очевидность такого вращения образованием смены времён года на Земле. Затем это сопряжение в нашей полевой фазе пространства переходит во взаимно-центрическое сопряжение сферического и окружного объёмов пространства, что выражается в дипольном или восьмеричном полевом образовании (а объёмно – в квадрупольном образовании) оболочковой полевой сферы. Равенство же отношений сферического и окружного объёмов пространства, образованных каждой планетой, означает обращение взаимно-центрического вращения вокруг центра окружного объёма, что и образует окружной центр взаимно-центрической системы. 

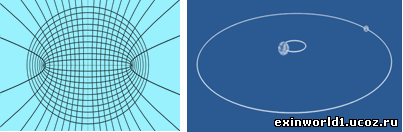
Обращение взаимно-центрического вращения вокруг центра окружного объёма означает, что окружной центр (воспринимаемый в гелиоцентризме неким «барицентром») образуется рядом с ведущим или с доминантным телом в системе. При этом наличие магнитного поля, – это один из основных признаков ведущего или доминантного тела во взаимно-центрической системе. Кроме того, вращение планеты и звезды (в составе их взаимно-центрической или двойной системы) вокруг окружного центра и образует их вращение вокруг оси. А обращение взаимно-центрической орбиты вокруг окружного центра, находящегося рядом с ведущим телом в двойной системе как раз и образует восприятие или иллюзию двухфокусной эксцентричной орбиты (относительно ведущего или доминантного тела) по первому закону И. Кеплера из-за полевого тяготения в нашей массовой фазе пространства к одно-центровому вращению. Этим эллиптические координаты (см. рисунок ниже слева) можно назвать искривлением исходной взаимно-центрической полевой окружности по причине образования одинарного центра окружного объёма нашего массового полевого пространства. Наглядность такого инверсионного вращения проявляется в двойной системе Плутона и Харона (см. рисунок ниже справа).
     

Первое требование Н. Коперника можно понимать и так, что не может быть вообще какого-либо одного центра для всех планетных орбит. Этим и наблюдаемая конфигурация планет – это иллюзия восприятия одно-центрового планетного вращения. Действительно, полное вращение (в радианном выражении «2пи») вокруг точки, как центра окружности, или вокруг одной оси невозможно в свободном пространстве космоса. Ведь нельзя закрепить в свободном полевом пространстве точку или ось. Потому и в космических наблюдениях видят вращения двойных систем, а не вращения одного тела вокруг другого. Но, исходя из неверного понимания тяготения и гравитации притяжением назначают при этом опять один (причём и одинарный) центр для двойных систем в виде некоего «барицентра» или «центра масс», нарушая этим требование Н. Коперника. 

Более того, не берётся в расчёт то, что обозначение у этой системы центра тяжести (чем и есть фактически «центр масс») абсурдно в невесомости космоса. Абсурдно потому и назначение «центром масс» точки, находящейся внутри космических тел (например, внутри тела Земли), поскольку это исключает возможность их вращения вокруг оси. Т.о., даже полевая структура падения с образованием дуги падения полевой окружностью, длина которой равна «дуговому» радиусу (полевому радиусу в виде дуги), проявляя этим иллюзию некоего «равноускоренного» падения, говорит о несоответствии наблюдаемой нами картины мира её полевой реальности. Отсюда и иллюзия конфигурации планет в виде их отдельного от Земли захода за Солнце, и, например, иллюзия вращения удалённых звёздно-планетных систем (считаемых и галактиками, и некими двойными, и тройными звёздами), как их годового вращения, что есть в реальности движением системы окружных центров звезды.

Вот потому при описании чрезвычайных ситуаций с падением с большой высоты вместо абсурда конечной скорости, набранной из-за некоего ускорения падения, пишут уже об «установившейся скорости», постоянной на всём пути падения, «объясняя» этот факт лобовым сопротивление воздуха, якобы уравновешивающим «ускорение» падения. При этом не обращается внимание, что в таком случает и падение прекратилось бы, поскольку «уравновешиваться» могут только силы, а не сила и «ускорение». По причине действия формулы «h=g₀*t²/4» с высот более 19,6 метров подобно признаётся и тот факт, что сила падения с небоскрёба и с самолёта (с высотой 10 км.) будет одинаковой (см. 33).

2. Частотно-контурное строение вещества и его квантовый переход. (Книга 4-я теории различения). Филиппов В.В.2014.

5.Взаимно-центрическое тяготение пространства (Космофизика теории различения), Том I (Книга 5-я Теории различения).