1. Что такое «солнечные сутки» Меркурия.
Верхние планеты в основном наблюдаемы уже в сферическом пространстве (что уже полностью относится к большим планетам). Потому внешние орбиты верхних планет изображаемы отдельно в виде эллипса (из-за их внутренних мутуальных орбит) относительно солнечно-земного взаимно-центрического центра. Также отдельно изображаемы и внутренние взаимно-центрические орбиты планет. Отношение же центра эллипса внешней орбиты верхних планет к Солнцу в гелиоцентризме не только противоречит первому закону Кеплера (поскольку Солнце находится лишь в одном из фокусов их внешних орбит), но – и их вешним орбитальным периодам. Напомним, что в гелиоцентризме примерно в полтора раза большее расстояние Марса от Солнца (чем у Земли) должно было бы означать и такое же превышение его орбитального периода. Но орбитальный период Марса в среднем в два раза больше земного, что и соответствует взаимо-центризму, где Марс имеет и примерно в два раза большее расстояние от солнечно-земного центра. Внешний же или в данном случае синодический период Венеры (как внутренней по отношению к Земле) более чем в полтора раза больший, чем земной годовой период, также не увязывается с гелиоцентризмом.
Но такой период означает и то, что нижние планеты, наблюдаясь, наоборот, в основном в окружном пространстве (точнее – в переходном пространстве расслоений), потому получают в их наблюдении слитные внешние и внутренние орбиты (или слитные экс – и инциклы), т.е. – в виде разомкнутой спирали. Цельная же их внешняя эллипсоидная орбита на мутуальной планетной оси вокруг солнечно-земного центра относится уже к непосредственно не наблюдаемому сферическому пространству (а потому имеет и обратное направление вращения относительно нашего пространства). Ведь в свободном пространственном вращении космоса не возможны жёсткие связи, что и проявляет реальным образом параллакс вращения.
В этом и состоит сложность различения вращения нижних планет. Согласно взаимно-центрической планетной системе Меркурий, как и Луна, своё внутреннее взаимно-центрическое вращение совершает в обратном направлении, чем солнечно-земное вращение. Но, в отличие от Луны, обратное вращение получает вся внешняя сфера системы Меркурия с его планетной сферой смещения, с которой он образует взаимно-центрическое вращение. Меркурий, как и все планеты, вращается в центре своей внутренней гравитонной планетной сферы (она изображена на рисунке ниже коричневым цветом). При этом его внешняя планетная сфера, как и у Венеры, катится изнутри по представимому или виртуальному орбитальному кольцу, образующемуся вследствие взаимодействия сферических пространственных слоёв или фаз. Качение же изнутри объясняется выходом внешней планетной сферы Венеры (она изображена на рисунке ниже зелёным цветом) за солнечно-земной центр на величину радиуса внешней центральной полевой сферы или на величину около 0,049 «а.е.».
Этим фактом и образуется внутренняя центральная полевая сфера (как центральная точка Лагранжа в понимании теорией различения) размером или диаметром лишь около 0,02 «а.е.», придающая минимальный эксцентриситет орбите Венеры величиной соответственно лишь около 0,01 а.е. (на рисунке залита белым цветом). Потому она (эта сфера) и составляет с внутренней планетной сферой Венеры внутреннее взаимно-центрическое вращение, но качением относительно неё изнутри. Также и внешняя сфера системы Меркурия заходит за солнечно-земной центр и на подобную величину (о чём речь дальше), а потому также катится относительно сферы системы Венеры изнутри. При этом внутренняя полевая сфера смещения Меркурия (изображена на рисунке голубым цветом) образуется за счёт смещения внутренней планетной сферы Меркурия от внешней контурной планетной сферы Венеры, также заходящей за солнечно-земной центр. О существовании внутри орбиты Меркурия относительно Солнца либо планеты, либо эквивалентного ей кольца некоего конденсированного вещества, как, например, пояса метеоритных тел, высказывал в своей гипотезе французский учёный У.Леверье ещё в 19-м веке. Полевая сфера смещения во внешней полевой сфере системы Меркурия, таким образом, и есть подтверждением указанной гипотезы.
Солнечная же полевая сфера как бы затягивает орбитальное вращение Меркурия вокруг солнечно-земного центра одновременно и во вращение вокруг Солнца. Полевая сфера смещения образует магнитное поле Меркурия. В таком взаимно-центрическом качении планетная сфера Меркурия совершает внутреннее орбитальное вращение против хода часовой стрелки при взгляде с севера Земли, но с прямым вращением Меркурия вокруг его оси. У Венеры же это происходит зеркально наоборот - прямое внутреннее орбитальное вращение с обратным вращением вокруг оси. Это и значит, что Солнце на Меркурии восходит, как и на Земле на востоке или слева, если встать к нему лицом. Однако внешнее прямое вращение (одновременно и относительно Солнца, и относительно солнечно-земного мутуального центра) идёт на фоне обратного внутреннего орбитального вращения Меркурия. Этим и объясняется, что "Солнце после восхода вдруг останавливается, поворачивает обратно и заходит почти в той же точке, где взошло" с повторением этого явления и на заходе.
Т.о., приведённый «эффект Навина» на Меркурии - это следствие наложения прямого внешнего орбитального вращения Меркурия относительно Солнца и относительно солнечно-земного центра на внутреннее орбитальное вращение Меркурия на общей мутуальной планетной оси, как происходящее в обратном направлении, чем солнечное вращение. Кстати, прямое внешнее орбитальное вращение, проходящее в окружном пространстве и относительно Солнца, не даёт установить сам факт внутреннего орбитального вращения, воспринимаемого лишь в виде эксцентриситета меркурианской орбиты.
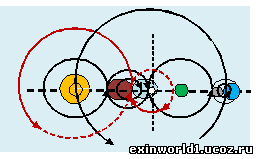
В исследованиях Меркурия определили, что его звёздные сутки составляют 2/3 от его годового вращения. Но ведь стоит обратить внимание и на то, что синодический или внешний орбитальный период Меркурия (116 земных суток) также составляет около 2/3 от так называемых солнечных меркурианских суток, как возвращения определённой точки поверхности Меркурия в его перигелий. И равны они двум периодам по 88 земных дней (176 дней), называемым в теории гелиоцентризма меркурианскими годами. И то, что синодический период Меркурия не завершает период его возвращения в перигелий, состоящий из 2-х меркурианских якобы годов, как из трёх его звёздных суток, означает только то, что есть третье вращение Меркурия - его внешнее орбитальное вращение, состоящее примерно из полутора его синодического периода, и которое именуется некими солнечными сутками. Вот именно этот период (176 земных дней) и есть его годовым вращением. А то, что называется годовым или сидерическим периодом (88 земных дней), означает длительность внутреннего взаимно-центрического вращения Меркурия с его полевой сферой смещения. В абсурде же гелиоцентризма, называя период внутреннего орбитального вращения Меркурия периодом обращения его вокруг Солнца, при этом обозначают и другой орбитальный период, как синодический период (около 116-и земных суток), не говоря уже о введении ещё больших неких солнечных суток. Это и означает отсутствие различения вращения Меркурия и планетного вращения вообще в системе гелиоцентризма.
Т.о., совмещённая орбита Меркурия, показанная на рисунке красным цветом, представляет собой разомкнутую спираль, состоящую на 2/3 из вращения относительно Солнца и на 1/3 – из вращения вокруг солнечно-земного мутуального центра (идущего уже в обратном направлении). Пространственный же поворот на радианную величину «пи» в сферическо-окружном переходе образует этим полную орбитальную окружность и вокруг солнечно-земного центра, и вокруг вращения солнечной сферы (эти продолжения орбитальных окружностей показаны красным пунктиром). В таком виде совмещённой орбиты Меркурия и заключается взаимно-центрический параллакс его орбиты. А поскольку образование таких двух орбит в переходном пространстве расслоения идёт одновременно, то 2/3 годового периода длительностью в 176 дней (называемого солнечными сутками) или период около 116 земных суток относится полностью к вращению вокруг солнечной сферы . А 1/3 годового периода (около 59-и земных суток) – полностью к вращению вокруг солнечно-земного центра. Образованием такой орбитальной восьмёрки и объясняется, что синодический или конфигурационный период Меркурия (как возвращение его в ту же точку соединения с Солнцем) составляет 2/3 от общего годового периода. При этом 2/3 от годового периода Меркурия – это примерно и 1/3 от продолжительности земного года, что подтверждает синхронность общего солнечно-земного планетного вращения в сферическом пространстве. Вращение Меркурия является, таким образом, связующим звеном между начальным вращением солнечной сферы и вращением общей солнечно-земной системы. Внешняя орбита Меркурия на рисунке здесь показана вращением центра его внутренней орбиты (что подобно вращению центра эпицикла в теории Птолемея), исключающим эксцентриситет орбиты. Подобную внешнюю орбиту можно применять и для других планет, в том числе, - и для совместной солнечно-земной орбиты (как инвариантной орбитальной плоскости в восприятии гелиоцентризма)
2. Реальное вращение Меркурия и переходное солнечно-земное расстояние.
Годовое вращение нижних планет - это их внешние взаимно-центрические или мутуальные орбиты. Для нижних планет они и исходят из их внешнего периода, как синодического (у Венеры они и равны ему). Для верхних же планет их внешнее вращение - это их сидерический период, а годовой период вращения, наоборот, исходит из их внутреннего или синодического периода, для больших планет примерно равного земному году (подчёркивая наличие синхронного частотного вращения и вращение мутуальной планетной оси). При этом у Марса годовое вращение, относясь к внутреннему вращению, как к синодическому вращению, образуется за счёт внешнего или сидерического периода вокруг солнечно-земного центра. Потому эксцентриситеты внешней орбиты планет, в том числе и Меркурия, в действительности и относятся к вращению вокруг этого ключевого мутуального центра, а не к Солнцу, объясняясь их внутренними взаимно-центрическими или мутуальными орбитами. Внутренним взаимно-центрическим вращением Меркурия, происходящим на фоне его внешнего орбитального вращения вокруг Солнца, объясняется и эффект повышения угловой скорости внешнего орбитального вращения на участке вблизи перигелия Меркурия, как накладывание или совмещение внешнего и внутреннего вращения (см. рисунок ниже слева).
 По рисунку видно, что вблизи перигелия, образующегося из-за вращения Меркурия по внутренней взаимно-центрической орбите, обратное внутреннее вращение Меркурия приводит к тому, что его внутренняя орбитальная скорость складывается со скоростью его внешнего орбитального вращения относительно Солнца. Наложением внутреннего орбитального вращения Меркурия на его внутреннее орбитальное вращение объясняется и движение Солнца вблизи перигелия в течение тех же восьми земных дней в обратном направлении для «меркурианского» наблюдателя. Потому эти эффекты наряду с последовательностью фаз Меркурия, подобных лунным фазам и показывающих внутренне вращение по направлению хода часовой стрелки, свидетельствует и об обратном или ретроградном внутреннем вращении Меркурия. Период образования полной внешней орбиты Меркурия (называемый его солнечными сутками) соответствует его двум внутренним периодам или периодам вращения по внутренней орбите, состоящим их трёх звёздных суток (как вращений Меркурия вокруг его оси), т.е. одни меркурианские сутки составляют 2/3 от его внутреннего орбитального периода. При этом и синодический период, как период изменения видимого положения планеты относительно Солнца, примерно составляет 2/3 от внешнего орбитального периода Меркурия. Вот потому долгое время и считалось, что Меркурий, как и Луна, обращён к Солнцу одной и той же стороной.
Т.о., истинный годовой период Меркурия (период возвращения в перигелий, как период неких солнечных суток) в восприятии окружного (непосредственно нами наблюдаемого) пространства состоит из 2/3 обращения вокруг Солнца, воспринимаемого синодическим периодом, и - из 1/3 вращения вокруг солнечно-земного центра. Это значит, что, как и у Венеры, внешняя орбита Меркурия из-за параллакса вращения в свободном космическом пространстве, как в окружном и в переходном пространстве, - это подобие разомкнутой спирали, что и изображено на рисунке выше красной линией. При этом в отличие от Марса и больших планет эта разомкнутая спираль реальна для окружного пространства, а не является лишь следом в переходном пространстве (воспринимаемым галактическими рукавами). А поскольку вращение вокруг Солнца и солнечно-земного центра идёт совместно, то разомкнутую спираль орбиты Меркурия (как центра его внутренней орбиты) можно изображать и орбитальной восьмёркой, также изображённой на рисунке выше. Здесь 2/3 годового периода (называемого солнечными сутками Меркурия) относится к вращению вокруг Солнца и к синодическому периоду, а 1/3 – к вращению вокруг солнечно-земного центра.
Потому заход Венеры и Меркурия за Солнце реален (точнее реально наблюдаем), но - только в окружном пространстве. В сферическом же или истинном пространстве орбита Меркурия, как и у других планет, - это эллипсоидная окружность вокруг солнечно-земного центра, поскольку в этом пространстве вращение происходит с постоянной частотой вращения или с постоянной угловой скоростью, т.е. – на общей мутуальной оси планет. Но при этом наблюдается свой собственный орбитальный период из-за вращательного параллакса в свободном пространстве космоса. И только для больших планет (поскольку синодический период для них становится окончательно периодом внутреннего взаимно-центрического вращения), внутренний орбитальный период становится примерно равным земному году, как периоду солнечно-земного исходного вращения. Потому можно сказать, что для нижних планет взаимно-центрический параллакс вращения планет в открытом космосе реален, для верхних же планет он только воспринимаем, как и их попятное движение.
Исходя из этого, на примере вращения нижних планет – Меркурия и Венеры можно наблюдать явный сферическо-окружной пространственный переход. Употребляемое среднее расстояние Меркурия от Солнца – 0,383 «а.е.» относится к окружному или - к непосредственно наблюдаемому пространству. В сферическом же пространстве (из-за радиуса вращения Земли, как половины его расстояния до Солнца) это расстояние в два раза меньше – около 0,191 «а.е.» В связи с этим расстояние Земли до нашей звезды в переходном пространстве – это среднее расстояние между сферическим и окружным радиусом. Потому средний размер орбитального вращения Земли (относительно гелиоцентризма и взаимо-центризма), как его переходное расстояние от Солнца или как переходный диаметр солнечно-земной орбиты – это 0,75 «а.е.».
В связи с этим реальный диаметр внешней орбиты Меркурия вокруг солнечно-земного центра (как середины расстояния 0,75 «а.е») относительно его расстояния от Солнца в сферическом пространстве (0,191 «а.е.») составляет 0,368 «а.е.», т.е. – почти половину переходного диаметра солнечно-земной орбиты. В связи с этим и истинный год или внешний орбитальный период Меркурия (называемый солнечными сутками) равен примерно половине земного года – 176 дней. Подобно и У.Рассел оценивает расстояние Земли от Солнца примерно в 0,6 «а.е» (см.& №2.10), что связано с изменением расстояния Венеры от Солнца в сферическом пространстве с 0,72 «а.е.» на вдвое меньшую величину – 0,36 «а.е.». В таком случае минимальное расстояние от Земли до Венеры около 0,28 а.е. также в сферическом пространстве, как расстояние постоянное (относящееся к мутуальной планетной оси) и даёт расстояние примерно в 0,6 а.е. или 0,64 «а.е.» (0,28+0,36). Но, судя по орбитальным периодам нижних планет, такое расстояние не отвечает действительности, наблюдаемой с Земли в виде разомкнутой спирали совместной (внутренней и внешней) орбиты нижних планет, обозначающей сферическо-окружной пространственный переход. При этом надо обратить внимание и на то, что внешняя планетная сфера мутуальной системы «Земля-Луна» определяется, исходя из изменения начальных (после эволюционной «протовспышки» света) полевых планетных сфер Солнца и Земли до нынешнего состояния. Это изменение означает «чистые» (без 5-и дней противостояний и равноденствий) солнечные сутки числом 360. Отношение 1/361, как один годовой оборот Земли, дающий 360 нынешних суток при расстоянии до Солнца в 1 «а.е.» в окружном пространстве, и означает радиус внешней земной полевой сферы размером 0,00277 «а.е.».
О приведённой пропорции свидетельствует факт почти одинаковых соотношений именно диаметров Солнца к диаметру Земли (1390000/1275=109) и солнечно-земного расстояния (выходит, что как также диаметра солнечно-земной орбиты) к диаметру Солнца (149600000/1390000=108). Т.о., вращение Меркурия и Венеры, хотя и начинается вращением солнечной сферы, но – в рамках единого солнечно-земного вращения. При этом в окружном пространстве средний радиус совместной (внутренней и внешней) орбиты Меркурия относительно солнечно-земного центра, составляющий 1/3 от всей его наблюдаемой с Земли орбиты, равен около 0,117 «а.е» (0,5-0,383, как среднее расстояние Меркурия от Солнца в окружном пространстве). Этим в сферическом пространстве (относительно окружного пространства) Меркурий в среднем занимает наиболее близкое к Земле расстояние. Потому и считается, что Меркурий, несмотря на то, что есть первой планетой от Солнца в среднем – это наиболее близкая к Земле планета. На окружной же части своей орбиты уже относительно Солнца, составляющей 2/3 от всей орбиты, Меркурий, наоборот, наиболее удалён от Земли, поскольку имеет здесь меньшее расстояние от Солнца в 0,191 «а.е.», как уже в сферическом пространстве. А это означает, что сферическое и окружное пространство существуют неразрывно друг в друге, несмотря на сферическо-окружной пространственный переход.
3. Планетные полевые сферы мутуальной системы «Солнце-Меркурий».
Не различение инверсии расстояний в космосе из-за сферическо-окружного пространственного перехода связано не только с применением неверной предпосылки гелиоцентризма. Дело в том, что расстояния до планет (как светил на наблюдаемой земной небесной сфере) определяются, исходя из их суточного или горизонтального параллакса, как угла, под которым из планеты, наблюдаемой на горизонте Земли, был бы виден экваториальный радиус Земли перпендикулярно к нему (см. рисунок ниже). Но параллакс – это и есть параллакс, как «изменение видимого положения объекта относительно удалённого фона в зависимости от положения наблюдателя». Потому это уже изначально есть некое усреднённое измерение, принимаемое за истинное положение вещей. При измерении расстояния до планеты практически не учитывается, в частности, и наклон земной оси. При этом фактически не различается и наклон эклиптики к небесному экватору от наклона земного экватора к плоскости земной орбиты, как измерения, имеющие разные точки наблюдения. В связи с этим фактически определялось расстояние лишь до Солнца и ближайших планет, Венеры и Марса (а в основном лишь до Венеры), как дающее наименьшую погрешность. Остальные же расстояния находились вычислением по третьему закону Кеплера, но опять же – исходя из схемы гелиоцентризма. И это, уже не говоря о плоском или окружном взаимно-центрическом параллаксе, дающем в наблюдении с Земли явные признаки вращения вокруг Солнца, отсутствующие в действительности (как отсутствует в действительности и попятное движение планет).
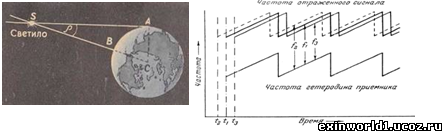 А при измерении расстояний до планет методом радиолокации с первого взгляда вроде бы объективно измерялось время, затрачиваемое отправленным сигналом на преодоление расстояния до планеты и обратно после его отражения (22). Но, во-первых, сферическо-окружной переход в космическом пространстве согласно физике различения означает и соответствующее изменение скорости распространения света и сигнала. А, во-вторых, хотя измеряемая разность частот исходящего сигнала и приёмного гетеродина изменялась одинаково по пилообразному закону и с задержкой на время распространения сигнала до планеты и обратно (см. рисунок выше справа), но «модуляция частоты гетеродина начиналась в момент t1, когда по расчёту отражённый сигнал должен был вернуться». Это значит, что измеряемые расстояния до планет и методом радиолокации исходили из уже принятого расстояния до них на основе гелиоцентризма. Потому и метод радиолокации в действительности был применён к измерению расстояния лишь до Венеры, причём - при её перигеи (наименьшем расстоянии от Земли), когда можно было напрямую следить за движением сигнала без всякого начала модуляции частоты гетеродина. Т.о., верными можно считать расстояния лишь для нижних планет (но с учётом их переходного расстояния от Солнца) и до Марса (с учётом его действительного эксцентриситета). Причём и эти расстояния необходимо оценивать в долях солнечно-земного расстояния, но никак - не в линейных километрах.
Эксцентриситет Меркурия в окружном пространстве, как его афелий и перигелий (минимальное и максимальное расстояние от Солнца) составляет соответственно 0,466 и 0,307 «а.е.». В связи с этим диаметр внутренней взаимно-центрической меркурианской орбиты составляет 0,159 «а.е.» (0,466-0,307). И, если в логичном предположении принять равенство внутренних полевых сфер Меркурия и его взаимно-центрической сферы смещения, как «чисто» полевой сферы, то внешняя полевая сфера Меркурия составляет в диаметре 0,318 «а.е.» (0,159*2), что и изображено на рисунке ниже (где внутренняя полевая сфера Меркурия показана коричневым цветом). Известен факт равенства звёздный суток Меркурия (периода его вращения вокруг оси при внутреннем орбитальном вращении) величиной примерно в 59 земных дней двум синодическим лунным месяцам (по 29,5 земных суток). Это обстоятельство также свидетельствует о единой мутуальной планетной оси и о единой частоте вращения в сферическом или исходном пространстве. Но это означает и то, что внешняя полевая сфера мутуальной системы Солнца (изображена на рисунке розовым цветом), воспринимаемая в её вращении вокруг Солнца центральной частью гелиосферы, получает вращение синхронно с лунным вращением, будучи в два раза меньше (0,159 «а.е.») внешней полевой сферы системы Меркурия. Внешняя солнечная полевая сфера в свою очередь совершает вращение качением относительно внутренней солнечной полевой сферы, проявляемой солнечной короной и образующей видимое тело Солнца (показано красным цветом). Этим мутуальная или взаимно-центрическая система «Солнце-Меркурий» предстаёт тройной системой. Внутренняя солнечная сфера образует средний период вращения внешних видимых слоёв Солнца, равный около 25,23 земных дней относительно лунного синодического периода обращения (среднее между 25,38 земными сутками, как сидерическим периодом, и 25,05 днями экваториального периода вращения Солнца вокруг оси). Этим соответственно в 1,169 раз меньше (29,5/25,23) должен быть диаметр внутренней солнечной сферы (показана на рисунке красной окружностью), т.е. – величиной около 0,136 «а.е.».
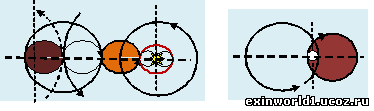 Сумма радиуса внутренней солнечной полевой сферы, диаметра внешней полевой сферы Солнца и радиуса внутренней сферы системы Меркурия (0,068+0,159+0.0795) даёт значение его перигелия 0,307 «а.е». Сумма же радиуса внутренней солнечной сферы (как наблюдаемого центра Солнца) и диаметров внешних полевых сфер Солнца и Меркурия (0,068+0,159+0,318), как величина 0,545 «а.е», показывает, почему внешняя сфера Меркурия, как и полевая сфера Венеры вращается как бы изнутри, а внутренняя орбита Меркурия ретроградная. Ведь полевая внешняя сфера Меркурия также заходит за солнечно-земной центр и на примерно такую же, как и у Венеры, величину (в окружном пространстве) – 0,045 «а.е», чем и образуется внутренняя полевая сфера смещения Меркурия. Внешняя полевая сфера Меркурия совершает взаимно-центрическое качение относительно внутренней полевой солнечной сферы (и одновременно относительно солнечно-земного центра), но - через качение по внешней солнечной сфере, что подобно вращению внешней сферы Марса в её качении относительно сферы нижних планет через её качение по лунно-земной сфере. При этом внешняя полевая сфера Солнца вращается уже только вокруг Солнца, образуя подобие кольцевой планетной сферы. Этим фактом, а также вращением внутреннего тела Солнца (гелиоида) объясняется более быстрое окружное вращение экваториальных областей Солнца, чем околополюсных областей, имеющих период как раз около синодического лунного периода. У обычного же вращающегося сферического тела наблюдается обратная картина (с меньшим периодом вращаются околоосевые области из-за меньшего радиуса сферы в этих областях). Этот факт подчёркивает и полевой характер солнечного и планетного вращения.
Т.о., внешняя полевая солнечная сфера (в отличие от планетных сфер) не является следствием качения вокруг друг друга внутренних солнечных сфер, а выступает отдельной полевой сферой, затягиваясь вращением внутренней солнечной полевой сферы и, в свою очередь, затягивая этим в это вращение и внешнюю полевую сферу Меркурия. Но спирально-возвратное вращение солнечно-земного центра с внутренним периодом вращения, равным действительному (а не наблюдаемому) периоду солнечной активности в 12 лет, образующее этим общее синхронное солнечно-земное вращение, наоборот, заставляет Меркурий одновременно вращаться и вокруг солнечно-земного центра. Этим вращение Меркурия и Венеры лишь обозначается относительно Солнца вследствие сферическо-окружного пространственного перехода. Относительно же внешнего или наблюдаемого с Земли вращения перехлёст внешних планетных сфер Меркурия и Венеры, примерно одинаково заходящих за солнечно-земной центр (см. рисунок выше справа), образует этим внешнюю центральную сферу, которую можно назвать сферой Лагранжа. При этом можно сказать, что вращение внешней планетной сферы Венеры (образующая окружности которой на общей мутуальной оси направлена в сторону солнечно-земного центра) как бы оттягивает на 1/3 орбитальное вращение Меркурия от вращения вокруг Солнца. Внешняя же планетная сфера Меркурия (окружность которой направлена в сторону Солнца), наоборот, как бы оттягивает уже на 1/2 орбитальное вращение Венеры от вращения вокруг солнечно-земного центра.
Источник:
Читать книгу 5-ю по теории различения (Тяготение пространства или астрофизика различения).
|



